JP Journal of Geometry and Topology
Volume 7, Issue 2, Pages 175 - 233
(July 2007)
|
|
INVARIANTS FOR CHAIN COMPLEXES OVER LOCAL ALGEBRAS
Lowell E. Jones (U.S.A.)
|
Abstract:
We consider chain complexes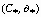 
over a local algebra R, where
each  is isomorphic to the direct sum of
finitely many principal
R-modules. If R is commutative or Noetherian (in addition to being
local), we are able to prove that such a chain complex is isomorphic to the
direct sum of a "minimal core" chain subcomplex with
"elemental" chain subcomplexes; the isomorphism types of these
summands are invariants of the isomorphism type of the given chain complex.
Examples of such chain complexes arise from group actions by finite groups on
finite CW complexes. In these examples the "minimal core" chain
complex turns out to be a topological invariant of the group
action. |
| Keywords and phrases: chain complexes, local algebras, group actions. |
| |
| Number of Downloads: 252 | Number of Views: 866 |
|
